¿Cuántos paquetes necesito para completar el álbum de figuritas de Qatar 2022?
En estos días tuvo bastante difusión un tuit mío en el que calculaba la cantidad de paquetes necesarios para completar el álbum de figuritas del mundial, suponiendo en distintos escenarios que uno no intercambia figuritas con nadie o que sí lo hace.
Coleccionando solo, se necesitan 1170 paquetes para tener 90% de probabilidad de completar el álbum.
— Federico Tiberti (@fedetiberti) August 23, 2022
Coleccionando de a dos (cambiando repetidas con otra persona), se necesitan 745 paquetes.
De a cinco, se necesitan 450.
De a diez, 340.
Hay que intercambiar! https://t.co/GciOZfd7Rm pic.twitter.com/cIrVOSZ7QQ
Voy a describir la simulación y mostrar el código que la genera. Primero, es importante aclarar que en esta simulación estoy partiendo de un supuesto clave: no existen las figuritas difíciles. Esto implica que todas las figuritas tienen la misma probabilidad de aparecer en un paquete. Sí, unos cuantos me cuestionaron este supuesto en las respuestas del tuit, pero Panini afirma que todas las figuritas son fabricadas en las mismas cantidades y no existen algunas más difíciles de encontrar que otras.
Una característica adicional del proceso aleatorio de muestreo de figuritas en paquetes, que desconozco, es si cada figurita es una selección aleatoria con reemplazo del conjunto total de 638 figuritas, o si es sin reemplazo hasta completar el paquete. Esto es, si una misma figurita puede aparecer más de una vez en un mismo paquete o no. Como no sé la respuesta a esto, voy a hacer las simulaciones suponiendo una cosa u otra.
Para empezar, podemos simular un paquete de figuritas como un muestreo aleatorio de cinco de las 638 figuritas posibles, sin reemplazo.
sample(1:638, 5, replace = FALSE)
## [1] 245 285 298 220 315
Podemos simular, digamos, 100 paquetes, de la misma forma:
paquetes100 <- unlist(lapply(vector("list", 100),
function(x) if (length(x) == 0) sample(1:638, 5, replace = FALSE) else x))
paquetes100
## [1] 464 513 11 394 92 83 418 19 2 506 255 601 520 583 306 238 208 47
## [19] 563 283 414 556 517 116 582 57 471 505 605 186 206 4 304 555 97 199
## [37] 608 99 277 592 484 563 67 210 559 582 540 309 596 409 36 197 142 545
## [55] 64 366 132 25 481 350 128 145 500 370 218 339 543 474 232 550 346 300
## [73] 607 129 360 200 413 399 299 447 58 389 82 301 520 521 181 251 214 389
## [91] 140 185 461 442 538 257 444 368 516 20 184 232 166 65 293 555 43 268
## [109] 210 140 601 124 513 602 431 136 396 314 634 300 87 259 581 499 210 360
## [127] 10 276 143 214 422 121 344 165 202 27 629 73 531 272 579 630 511 444
## [145] 49 585 20 389 275 601 420 295 353 444 162 460 24 119 367 594 62 455
## [163] 436 109 330 170 483 109 523 500 74 45 352 284 166 419 198 100 103 433
## [181] 587 612 210 247 282 314 370 572 566 438 131 427 428 291 394 628 275 324
## [199] 460 552 410 169 216 189 434 496 63 410 593 413 238 430 439 173 34 125
## [217] 237 317 199 501 426 593 93 500 342 459 437 75 146 421 53 341 286 80
## [235] 512 270 104 71 339 351 13 412 230 279 607 119 247 526 303 548 505 253
## [253] 8 370 226 626 195 211 413 200 245 345 624 50 481 534 344 207 45 425
## [271] 169 540 421 325 17 472 330 473 386 138 531 487 134 31 62 478 317 305
## [289] 273 179 281 413 148 241 445 167 322 278 14 571 273 301 556 280 387 607
## [307] 287 116 191 384 19 269 255 525 114 78 226 347 597 138 349 258 470 105
## [325] 297 416 302 52 94 488 73 462 252 474 386 638 234 318 138 80 459 402
## [343] 141 52 143 87 299 516 108 33 257 528 509 270 312 231 626 127 30 9
## [361] 484 613 302 15 125 418 198 96 337 548 437 260 29 532 55 536 299 107
## [379] 207 495 57 244 269 209 511 9 189 67 406 552 264 625 246 68 480 542
## [397] 145 70 545 344 300 331 581 189 130 185 195 485 460 270 374 538 273 318
## [415] 603 92 424 76 183 283 584 172 548 625 387 223 229 188 358 311 505 579
## [433] 76 536 427 355 91 452 238 173 1 366 569 612 200 176 334 287 137 543
## [451] 343 143 383 302 233 101 104 231 416 349 145 23 482 413 477 86 367 559
## [469] 496 282 181 433 5 634 394 330 472 635 535 115 21 143 484 25 370 14
## [487] 489 340 583 573 314 590 135 599 451 310 525 555 111 43
Se puede ver fácilmente que algunos números se repiten. Con la función table() podemos ver cuántas veces se repite cada elemento en el vector de números de figuritas:
paquetes100 %>% table()
## .
## 1 2 4 5 8 9 10 11 13 14 15 17 19 20 21 23 24 25 27 29
## 1 1 1 1 1 2 1 1 1 2 1 1 2 2 1 1 1 2 1 1
## 30 31 33 34 36 43 45 47 49 50 52 53 55 57 58 62 63 64 65 67
## 1 1 1 1 1 2 2 1 1 1 2 1 1 2 1 2 1 1 1 2
## 68 70 71 73 74 75 76 78 80 82 83 86 87 91 92 93 94 96 97 99
## 1 1 1 2 1 1 2 1 2 1 1 1 2 1 2 1 1 1 1 1
## 100 101 103 104 105 107 108 109 111 114 115 116 119 121 124 125 127 128 129 130
## 1 1 1 2 1 1 1 2 1 1 1 2 2 1 1 2 1 1 1 1
## 131 132 134 135 136 137 138 140 141 142 143 145 146 148 162 165 166 167 169 170
## 1 1 1 1 1 1 3 2 1 1 4 3 1 1 1 1 2 1 2 1
## 172 173 176 179 181 183 184 185 186 188 189 191 195 197 198 199 200 202 206 207
## 1 2 1 1 2 1 1 2 1 1 3 1 2 1 2 2 3 1 1 2
## 208 209 210 211 214 216 218 223 226 229 230 231 232 233 234 237 238 241 244 245
## 1 1 4 1 2 1 1 1 2 1 1 2 2 1 1 1 3 1 1 1
## 246 247 251 252 253 255 257 258 259 260 264 268 269 270 272 273 275 276 277 278
## 1 2 1 1 1 2 2 1 1 1 1 1 2 3 1 3 2 1 1 1
## 279 280 281 282 283 284 286 287 291 293 295 297 299 300 301 302 303 304 305 306
## 1 1 1 2 2 1 1 2 1 1 1 1 3 3 2 3 1 1 1 1
## 309 310 311 312 314 317 318 322 324 325 330 331 334 337 339 340 341 342 343 344
## 1 1 1 1 3 2 2 1 1 1 3 1 1 1 2 1 1 1 1 3
## 345 346 347 349 350 351 352 353 355 358 360 366 367 368 370 374 383 384 386 387
## 1 1 1 2 1 1 1 1 1 1 2 2 2 1 4 1 1 1 2 2
## 389 394 396 399 402 406 409 410 412 413 414 416 418 419 420 421 422 424 425 426
## 3 3 1 1 1 1 1 2 1 5 1 2 2 1 1 2 1 1 1 1
## 427 428 430 431 433 434 436 437 438 439 442 444 445 447 451 452 455 459 460 461
## 2 1 1 1 2 1 1 2 1 1 1 3 1 1 1 1 1 2 3 1
## 462 464 470 471 472 473 474 477 478 480 481 482 483 484 485 487 488 489 495 496
## 1 1 1 1 2 1 2 1 1 1 2 1 1 3 1 1 1 1 1 2
## 499 500 501 505 506 509 511 512 513 516 517 520 521 523 525 526 528 531 532 534
## 1 3 1 3 1 1 2 1 2 2 1 2 1 1 2 1 1 2 1 1
## 535 536 538 540 542 543 545 548 550 552 555 556 559 563 566 569 571 572 573 579
## 1 2 2 2 1 2 2 3 1 2 3 2 2 2 1 1 1 1 1 2
## 581 582 583 584 585 587 590 592 593 594 596 597 599 601 602 603 605 607 608 612
## 2 2 2 1 1 1 1 1 2 1 1 1 1 3 1 1 1 3 1 2
## 613 624 625 626 628 629 630 634 635 638
## 1 1 2 2 1 1 1 2 1 1
Entonces, podemos definir como un éxito el caso en que (1) aparecen las 638 figuritas y (2) aparecen tantas veces cada una como personas estén intentando completar el album en el escenario que estemos simulando.
personas <- 1
exito <- ifelse(length(unique(paquetes100))==638 & min(data.frame(table(paquetes100))$Freq)>=personas, TRUE, FALSE)
exito
## [1] FALSE
En este caso, obviamente no completamos el album, ya que con 100 paquetes ni siquiera se llega a tener 670 figuritas. Para saber qué probabilidad tenemos de completar el álbum con, digamos, 600 paquetes, podemos hacer la misma simulación mil veces pero cambiando la cantidad de paquetes y ver cuántas veces nos alcanza con esos 600 paquetes para completarlo.
simulaciones <- 1000
personas <- 1
paquetes <- 600
exito <- NULL
for(j in 1:simulaciones){
figus<- NULL
for(k in 1:paquetes){figus <- c(figus, sample(1:638, 5, replace = FALSE))}
figus <- figus %>% table() %>% as.data.frame()
exito[j] <- ifelse(nrow(figus)==638 & min(figus$Freq)>=personas, TRUE, FALSE)}
exitos <- sum(exito)
exitos
## [1] 2
Con 600 paquetes, en 10000 simulaciones solo se llegó a completar el album 2 veces, lo que muestra que aunque no sea imposible sigue siendo extremadamente improbable conseguir las 638 figuritas distintas con 600 paquetes sin intercambio.
El paso siguiente es hacer las simulaciones para distintas cantidades de paquetes, para calcular la probabilidad de completar el álbum con distintos números de paquetes. Cuando terminan de generarse las simulaciones para cada número de paquetes (el loop interno), se guarda el porcentaje de simulaciones “exitosas” (o sea, en que se completó la cantidad deseada de álbumes) en un objeto que luego servirá para ver qué probabilida de éxito hay con cada cantidad de paquetes.
Como mencioné más arriba, primero haré las simulaciones suponiendo que no puede salir una misma figurita dos veces en un paquete, y luego suponiendo que cada figurita es independiente de las demás del paquete.
Suponiendo no independencia dentro del paquete
Suponiendo que cada figurita no es independiente de las otras dentro de un mismo paquete, cada figurita es una selección aleatoria sin reemplazo del conjunto de 638 figuritas posibles con probabilidad distribuida uniformemente, defino dos funciones. A partir de este supuesto, defino dos funciones, calcular_exito() y simular_paquete(). calcular_exito() toma como argumento la cantidad de paquetes que se está simulando, que es el producto de la cantidad de personas participando y la cantidad de paquetes que cada una compra, genera una selección aleatoria de esa cantidad de figuritas, y verifica si se completó la cantidad buscada de álbumes, devolviendo. La función simular_paquete() toma como argumentos la cantidad de personas participando, las cantidades de paquetes que se quieren simular y la cantidad de simulaciones que se quiere correr para cada número de paquetes. Corre estas simulaciones usando calcular_exito() y para cada número de paquetes define la probabilidad de éxito como el porcentaje de simulaciones que devolvieron TRUE como resultado de calcular_exito() sobre el total de simulaciones ejecutadas.
En este caso, empiezo corriendo 250 simulaciones por cada número de paquetes entre 1 y 1600 Para agilizar las simulaciones (que son bastante demandantes para la computadora), no simulo todos los números del intervalo sino solo los impares
calcular_exito <- function(packs){
figus<- as.data.frame(table(unlist(lapply(vector("list", packs),
function(x) if (length(x) == 0) sample(1:638, 5, replace = FALSE) else x))))
return(ifelse(nrow(figus)==638 & min(figus$Freq)>=personas, TRUE, FALSE))}
simular_paquete <- function(personas, paquetes, simulaciones){
packs <- personas*paquetes
resultado <- unlist(lapply(vector("list", simulaciones), function(x) if (length(x) == 0) calcular_exito(packs) else x))
resultado <- sum(resultado)/simulaciones*100
return(resultado)
}
personas=1
simulaciones=250
prob_completar <- unlist(lapply(seq(1, 1600, by=2), function(x) simular_paquete(personas=1, paquetes=x, simulaciones=250)))
completado <- data.frame(paquetes = seq(1, 1600, by=2), prob_completar = prob_completar)
Con este objeto ya generado, se puede graficar la probabilidad de éxito con cada número de paquetes:
completado %>% ggplot(aes(x=paquetes, y=prob_completar)) +
geom_point(alpha = 0.5, color="gray44", size=0.8) + theme_light() +
scale_x_continuous(breaks = seq(0, 2000, by=200)) +
scale_y_continuous(breaks = seq(0, 100, by=10),
labels=scales::label_number(accuracy=1, suffix="%")) +
labs(x="Cantidad de paquetes", y="Probabilidad de completar el album",
title = "Una sola persona") +
theme(axis.text=element_text(face="bold", size=12),
plot.title = element_text(face="bold", size=22),
axis.title = element_text(face="bold", size=14))
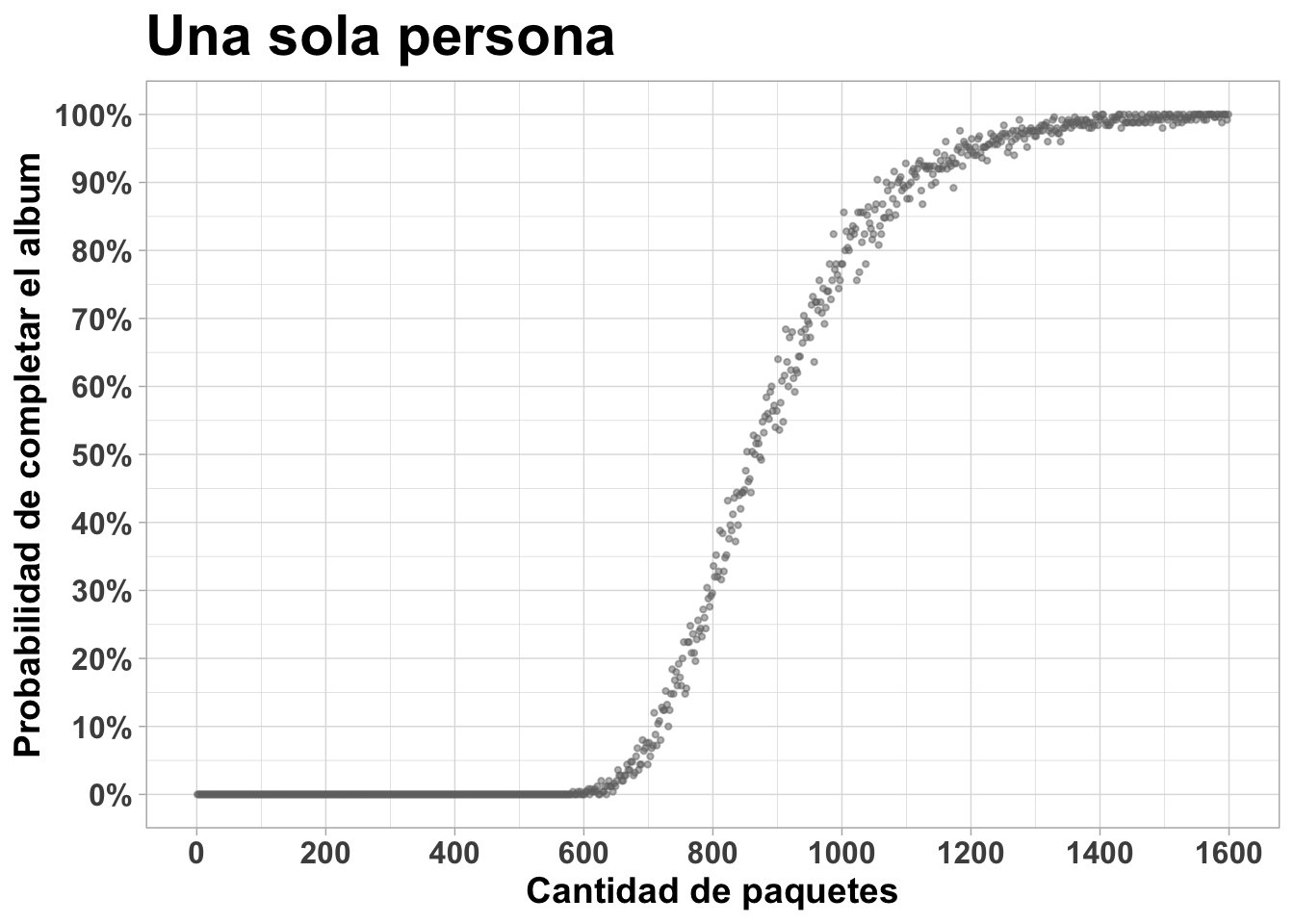
Se ve en el gráfico que se necesitan casi 1100 paquetes para llegar a una probabilidad de 90% de completar el álbum. Podemos repetir las simulaciones para 2, 5 y 10 personas:
personas=2
simulaciones=250
prob_completar <- unlist(lapply(seq(1, 1600, by=2), function(x) simular_paquete(personas=2, paquetes=x, simulaciones=250)))
completado2 <- data.frame(paquetes = seq(1, 1600, by=2), prob_completar = prob_completar)
personas=5
simulaciones=250
prob_completar <- unlist(lapply(seq(1, 1600, by=2), function(x) simular_paquete(personas=5, paquetes=x, simulaciones=250)))
completado5 <- data.frame(paquetes = seq(1, 1600, by=2), prob_completar = prob_completar)
personas=10
simulaciones=250
prob_completar <- unlist(lapply(seq(1, 1600, by=2), function(x) simular_paquete(personas=10, paquetes=x, simulaciones=250)))
completado10 <- data.frame(paquetes = seq(1, 1600, by=2), prob_completar = prob_completar)
El mismo gráfico de arriba para dos personas. Se ve que el número de paquetes en que la probabilidad de completar alcanza 90% baja a aproximadamente 700:
completado2 %>% ggplot(aes(x=paquetes, y=prob_completar)) +
geom_point(alpha = 0.5, color="gray44", size=0.8) + theme_light() +
scale_x_continuous(breaks = seq(0, 2000, by=200)) +
scale_y_continuous(breaks = seq(0, 100, by=10),
labels=scales::label_number(accuracy=1, suffix="%")) +
labs(x="Cantidad de paquetes por persona", y="Probabilidad de completar los albumes",
title = "Dos personas") +
theme(axis.text=element_text(face="bold", size=12),
plot.title = element_text(face="bold", size=22),
axis.title = element_text(face="bold", size=14))

Para cinco este número baja a apenas más de 400:
completado5 %>% ggplot(aes(x=paquetes, y=prob_completar)) +
geom_point(alpha = 0.5, color="gray44", size=0.8) + theme_light() +
scale_x_continuous(breaks = seq(0, 2000, by=200)) +
scale_y_continuous(breaks = seq(0, 100, by=10),
labels=scales::label_number(accuracy=1, suffix="%")) +
labs(x="Cantidad de paquetes por persona", y="Probabilidad de completar los albumes",
title = "Dos personas") +
theme(axis.text=element_text(face="bold", size=12),
plot.title = element_text(face="bold", size=22),
axis.title = element_text(face="bold", size=14))
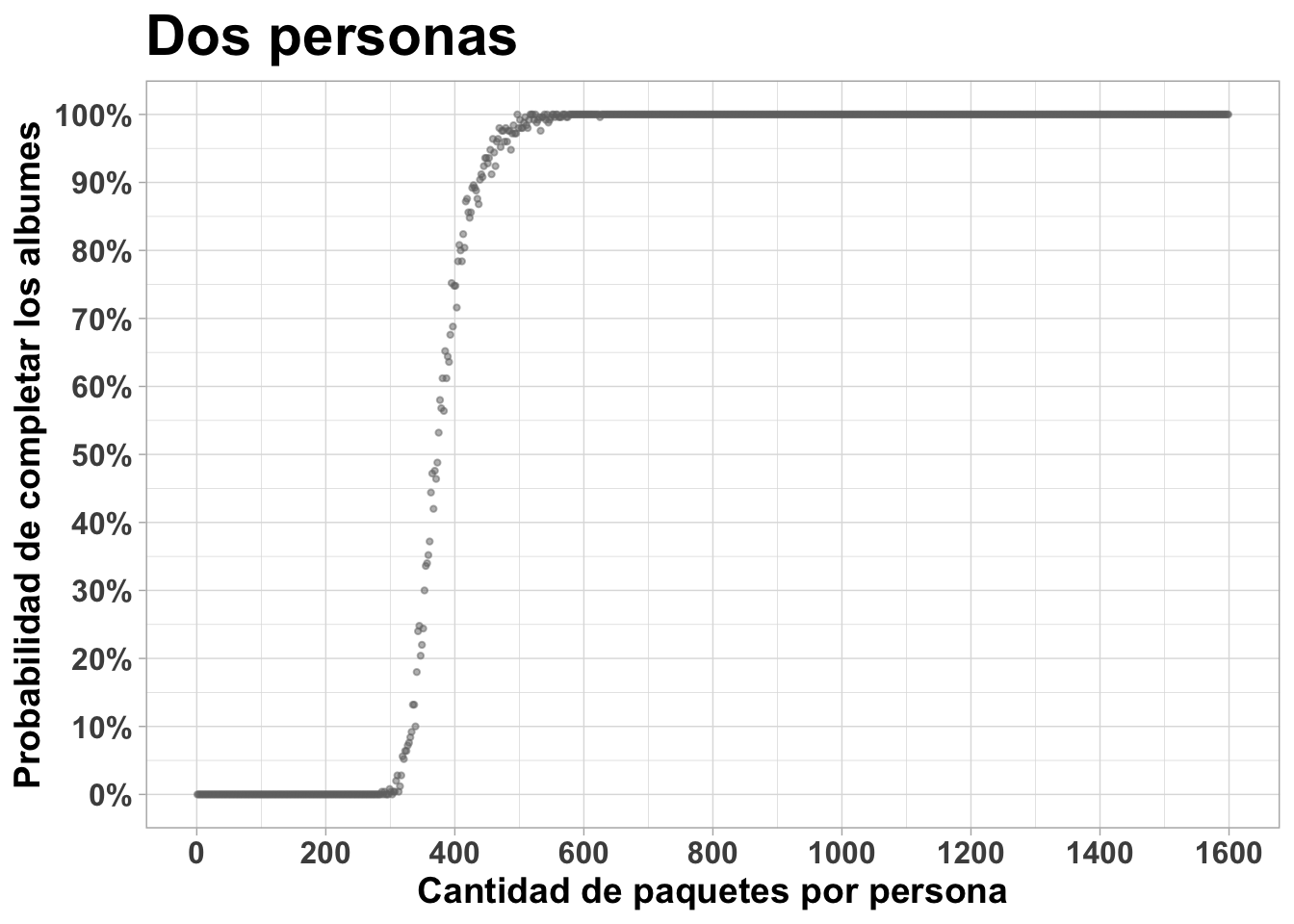
Y para diez es apenas más de 300:
completado10 %>% ggplot(aes(x=paquetes, y=prob_completar)) +
geom_point(alpha = 0.5, color="gray44", size=0.8) + theme_light() +
scale_x_continuous(breaks = seq(0, 2000, by=200)) +
scale_y_continuous(breaks = seq(0, 100, by=10),
labels=scales::label_number(accuracy=1, suffix="%")) +
labs(x="Cantidad de paquetes por persona", y="Probabilidad de completar los albumes",
title = "Dos personas") +
theme(axis.text=element_text(face="bold", size=12),
plot.title = element_text(face="bold", size=22),
axis.title = element_text(face="bold", size=14))
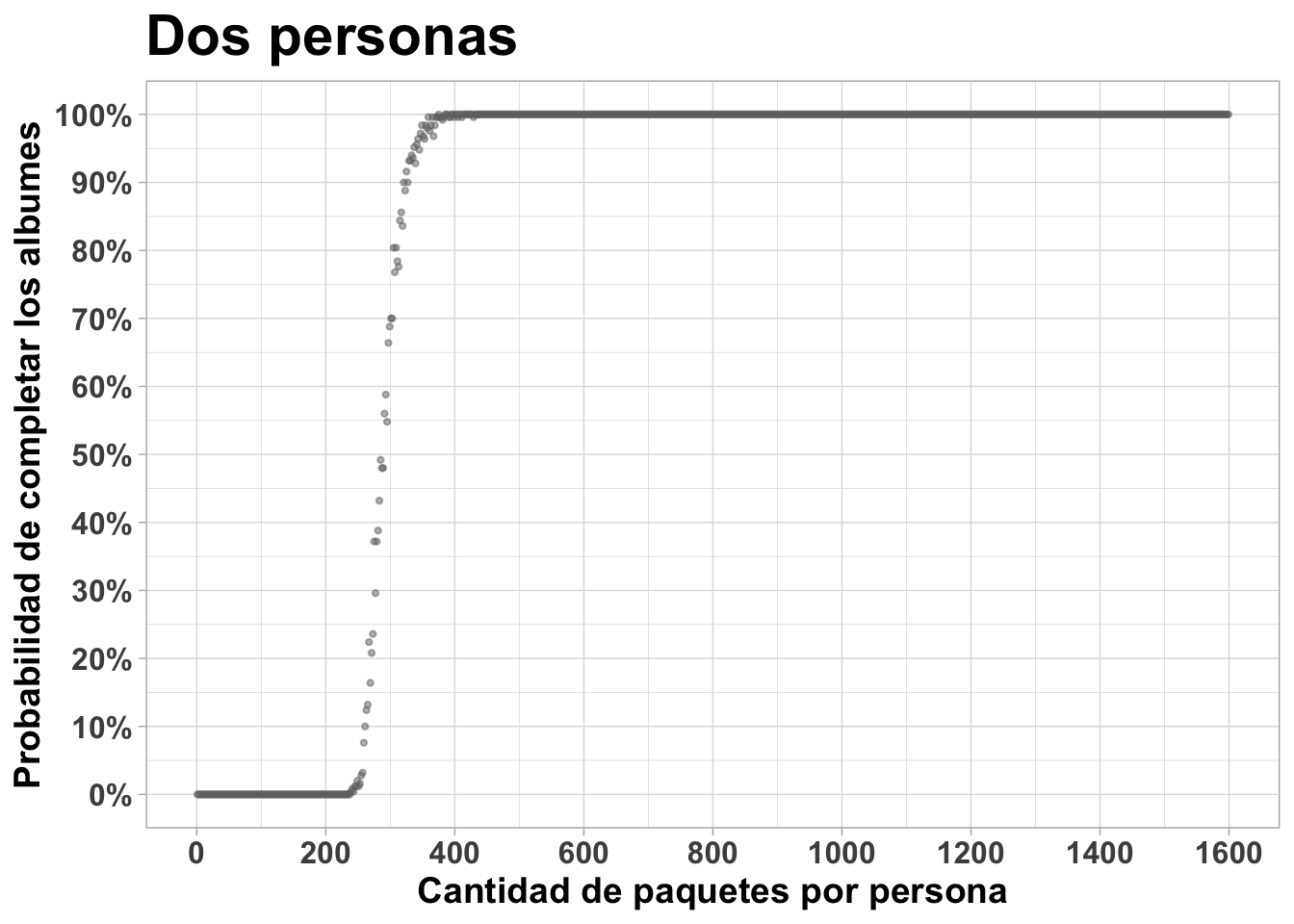
Suponiendo independencia dentro de un mismo paquete
Suponiendo que las figuritas pueden repetirse dentro de un mismo paquete, el ejercicio se simplifica bastante, aunque los resultados no sean muy distintos de los de arriba. Si cada figurita es independiente de las demás del mismo paquete, entonces el paquete deja de ser relevante a la hora de tomar la muestra de figuritas. Entonces, podemos simplemente, para cada nuúmero de personas y paquetes, tomar una muestra aleatoria con reemplazo de tantas figuritas como resulte del personaspaquetes5, y calcular el éxito de la misma forma de arriba.
personas <- 1
completado <- NULL
simulaciones <- 200
for(i in seq(1, 1600, by=2)){
exito <- NULL
for(j in 1:simulaciones){
figus <- as.data.frame(table(sample(1:638, i*personas*5, replace = TRUE)))
exito[j] <- ifelse(nrow(figus)==638 & min(figus$Freq)>=personas, TRUE, FALSE)}
simulacion <- data.frame(paquetes = i, prob_completar = sum(exito)/simulaciones*100)
completado <- rbind(completado, simulacion)}
personas <- 2
completado2 <- NULL
simulaciones <- 200
for(i in seq(1, 1600, by=2)){
exito <- NULL
for(j in 1:simulaciones){
figus <- as.data.frame(table(sample(1:638, i*personas*5, replace = TRUE)))
exito[j] <- ifelse(nrow(figus)==638 & min(figus$Freq)>=personas, TRUE, FALSE)}
simulacion <- data.frame(paquetes = i, prob_completar = sum(exito)/simulaciones*100)
completado2 <- rbind(completado2, simulacion)}
personas <- 5
completado5 <- NULL
simulaciones <- 200
for(i in seq(1, 1600, by=2)){
exito <- NULL
for(j in 1:simulaciones){
figus <- as.data.frame(table(sample(1:638, i*personas*5, replace = TRUE)))
exito[j] <- ifelse(nrow(figus)==638 & min(figus$Freq)>=personas, TRUE, FALSE)}
simulacion <- data.frame(paquetes = i, prob_completar = sum(exito)/simulaciones*100)
completado5 <- rbind(completado5, simulacion)}
personas <- 10
completado10 <- NULL
simulaciones <- 200
for(i in seq(1, 1600, by=2)){
exito <- NULL
for(j in 1:simulaciones){
figus <- as.data.frame(table(sample(1:638, i*personas*5, replace = TRUE)))
exito[j] <- ifelse(nrow(figus)==638 & min(figus$Freq)>=personas, TRUE, FALSE)}
simulacion <- data.frame(paquetes = i, prob_completar = sum(exito)/simulaciones*100)
completado10 <- rbind(completado10, simulacion)}
Abajo el gráfico para una persona. El 90% de probabilidad de completar el álbum se alcanza también cerca de los 1100 paquetes.
completado %>% ggplot(aes(x=paquetes, y=prob_completar)) +
geom_point(alpha = 0.5, color="gray44", size=0.8) + theme_light() +
scale_x_continuous(breaks = seq(0, 2000, by=200)) +
scale_y_continuous(breaks = seq(0, 100, by=10),
labels=scales::label_number(accuracy=1, suffix="%")) +
labs(x="Cantidad de paquetes", y="Probabilidad de completar el album",
title = "Una sola persona (figuritas independientes)") +
theme(axis.text=element_text(face="bold", size=12),
plot.title = element_text(face="bold", size=20),
axis.title = element_text(face="bold", size=14))

Abajo el gráfico para dos personas. El 90% de probabilidad de completar también se alcanza alrededor de los 700 paquetes.
completado2 %>% ggplot(aes(x=paquetes, y=prob_completar)) +
geom_point(alpha = 0.5, color="gray44", size=0.8) + theme_light() +
scale_x_continuous(breaks = seq(0, 2000, by=200)) +
scale_y_continuous(breaks = seq(0, 100, by=10),
labels=scales::label_number(accuracy=1, suffix="%")) +
labs(x="Cantidad de paquetes", y="Probabilidad de completar el album",
title = "Dos personas (figuritas independientes)") +
theme(axis.text=element_text(face="bold", size=12),
plot.title = element_text(face="bold", size=20),
axis.title = element_text(face="bold", size=14))
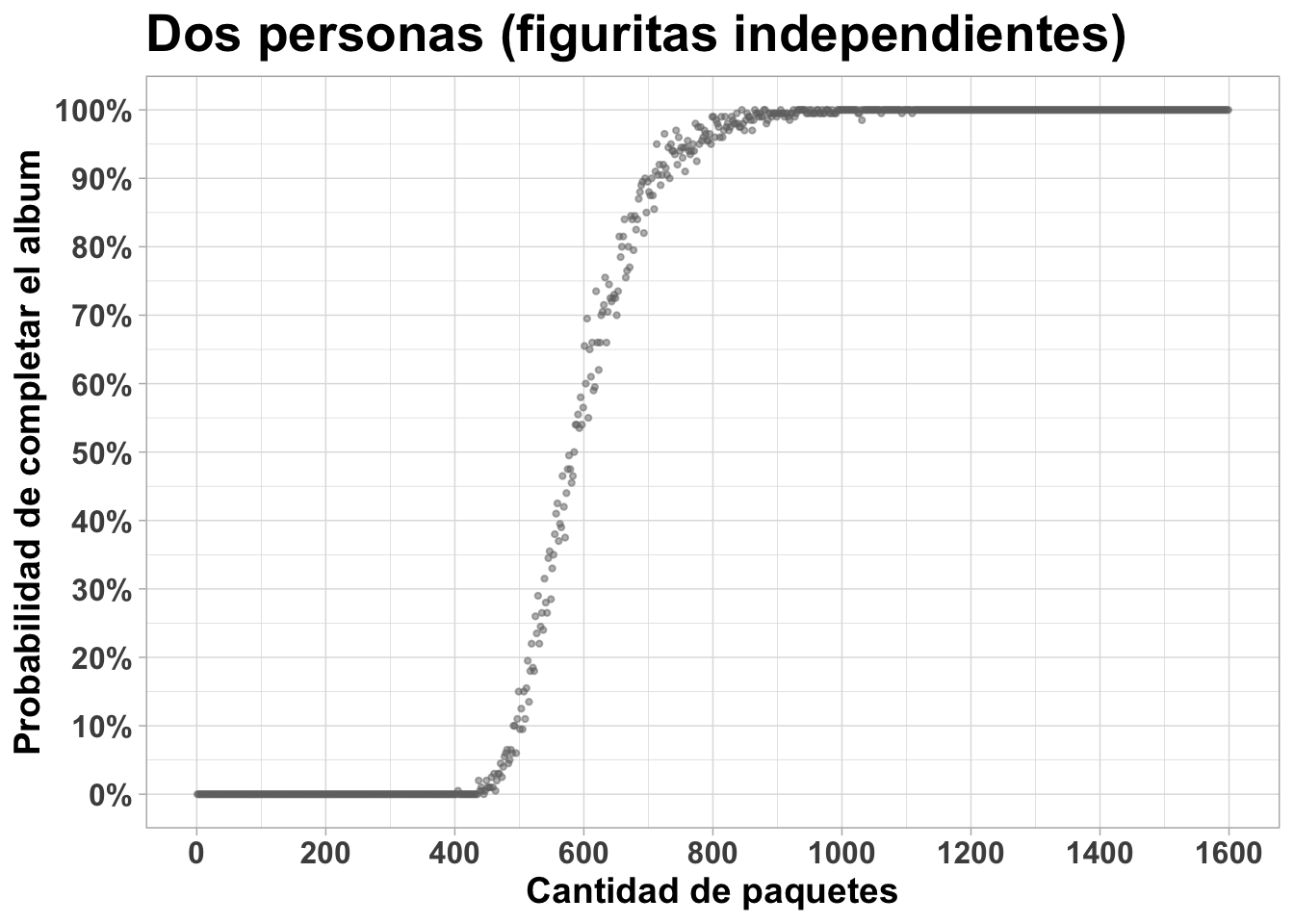
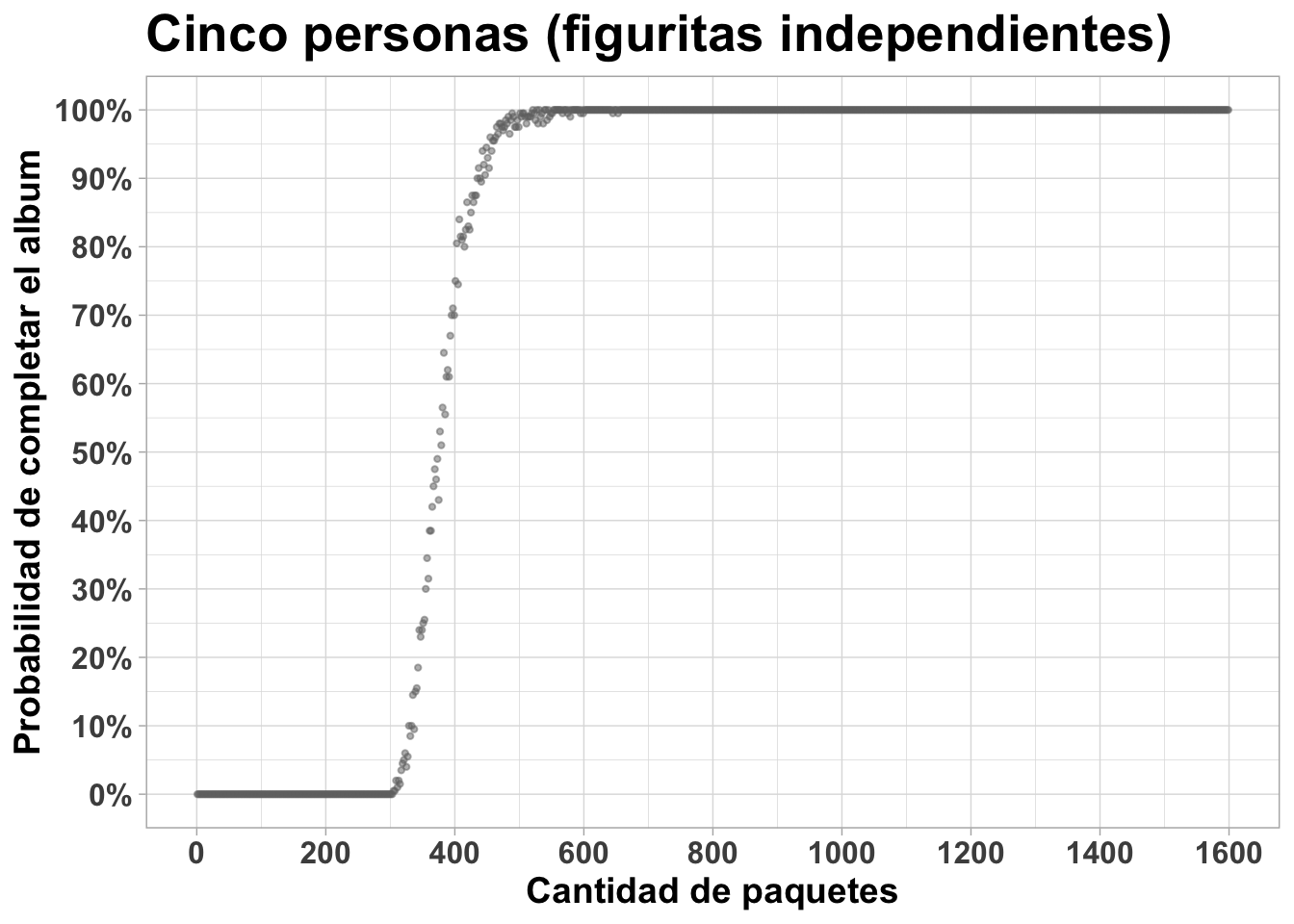
Abajo el gráfico para cinco personas. El 90% de probabilidad de completar nuevamente se alcanza cerca de los 400 paquetes.
completado5 %>% ggplot(aes(x=paquetes, y=prob_completar)) +
geom_point(alpha = 0.5, color="gray44", size=0.8) + theme_light() +
scale_x_continuous(breaks = seq(0, 2000, by=200)) +
scale_y_continuous(breaks = seq(0, 100, by=10),
labels=scales::label_number(accuracy=1, suffix="%")) +
labs(x="Cantidad de paquetes", y="Probabilidad de completar el album",
title = "Cinco personas (figuritas independientes)") +
theme(axis.text=element_text(face="bold", size=12),
plot.title = element_text(face="bold", size=20),
axis.title = element_text(face="bold", size=14))
Por último, el gráfico para diez personas. Al igual que con figuritas no independientes, el 90% de probabilidad de completar el álbum se alcanza con cerca de 300 paquetes.
completado10 %>% ggplot(aes(x=paquetes, y=prob_completar)) +
geom_point(alpha = 0.5, color="gray44", size=0.8) + theme_light() +
scale_x_continuous(breaks = seq(0, 2000, by=200)) +
scale_y_continuous(breaks = seq(0, 100, by=10),
labels=scales::label_number(accuracy=1, suffix="%")) +
labs(x="Cantidad de paquetes", y="Probabilidad de completar el album",
title = "Diez personas (figuritas independientes)") +
theme(axis.text=element_text(face="bold", size=12),
plot.title = element_text(face="bold", size=20),
axis.title = element_text(face="bold", size=14))
